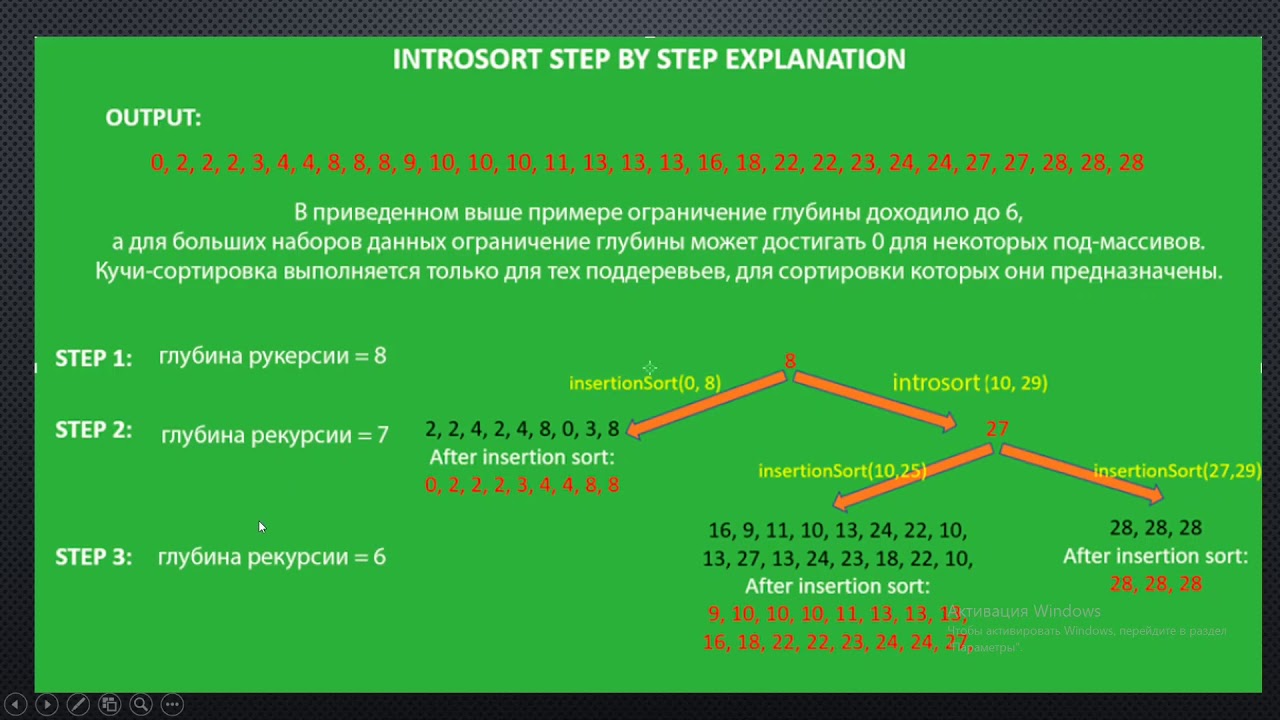
Introsort

Introsort ou introspective sort est un algorithme de tri par comparaisons. C'est une variante du tri rapide inventée par David Musser en 1997. Par rapport au tri rapide, Introsort a l'avantage d'avoir une complexité ${\displaystyle O(n\log n)}$ dans le pire cas.

Principe

L'algorithme de tri rapide est ralenti lorsque le pivot choisi se retrouve souvent au début ou à la fin du sous-tableau trié. Dans ce cas, la profondeur de récursion est en ${\displaystyle O(n)}$ et le temps total en ${\displaystyle O(n^{2})}$, ce qui est un temps comparable à un tri par sélection. Mais en moyenne, le tri rapide est efficace : sa complexité est ${\displaystyle O(n\log n)}$.

Introsort, pour pallier cet inconvénient, utilise un compteur de récursion. Ainsi il mesure au fur et à mesure la profondeur de récursion en cours (d'où le nom de l'algorithme). Quand la profondeur dépasse ${\displaystyle K\log n}$ où K est une constante, on trie le sous-tableau restant avec un algorithme dont la complexité est ${\displaystyle O(n\log n)}$ dans tous les cas, par exemple un tri par tas ou un Smoothsort.

Tout comme le tri rapide, Introsort peut être optimisé en triant les sous-listes de moins de 15 éléments avec un tri par insertion ou un tri de Shell, au fur et à mesure, ou à la fin (principe de Sedgesort).

Algorithme

Avec A: Tableau et n = Longueur(A)

Faire Introsort(A, 2*PartieEntière(Log2(n)) )

• Procédure Introsort (A : Tableau[Min..Max], ProfondeurLimite : Entier > 0)
  • Initialiser
    • CurMin := Min et CurMax := Max
    • Pivot := A[PartieEntière((Min Max) / 2)]
  • Répéter jusqu'à ce que CurMin > CurMax
    • Tant que A[CurMin] < Pivot, CurMin := CurMin 1
    • Tant que A[CurMax] > Pivot, CurMax := CurMax - 1
    • Si CurMin < CurMax alors Echanger(A[CurMin], A[CurMax])
    • CurMin = CurMin 1
    • CurMax = CurMax - 1
  • Si CurMax > Min
    • Si ProfondeurLimite = 1 alors faire Heapsort(A[Min..CurMax])
    • Sinon faire Introsort(A[Min..CurMax], ProfondeurLimite - 1)
  • Si CurMin < Max
    • Si ProfondeurLimite = 1 alors faire Heapsort(A[CurMin..Max])
    • Sinon faire Introsort(A[CurMin..Max], ProfondeurLimite - 1)

Voir aussi

• Tri rapide (quicksort)
• Tri par tas (heapsort)

Notes et références

• Portail des mathématiques
• Portail de l’informatique