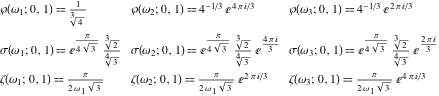Équation de Weierstrass

En mathématiques, une équation de Weierstrass, aussi appelée forme de Weierstrass, est une forme simplifiée de l'équation d'une courbe elliptique. La simplification de la forme générale

${\displaystyle y^{2} a_{1}xy a_{3}y=x^{3} a_{2}x^{2} a_{4}x a_{6}}$

à la forme de Weierstrass peut se faire par changement de variable, mais dépend de la caractéristique du corps commutatif K sur lequel la courbe elliptique est définie (c'est-à-dire le corps auquel appartiennent les coefficients a_k).

Il y a trois types d'équations de Weierstrass.

• Si la caractéristique de K est différente de 2 et 3 (ce qui inclut les cas où elle est nulle, par exemple quand K est le corps des réels, des complexes ou des rationnels) alors l'équation de Weierstrass pour une courbe elliptique est de la forme

${\displaystyle y^{2}=x^{3} ax b}$

où a, b sont des éléments de K.

• Si la caractéristique de K est 3 (par exemple si K est le corps fini à 3^r éléments) alors l'une des deux simplifications suivantes est applicable :

${\displaystyle y^{2}=x^{3} ax^{2} b}$ (cas ordinaire)

${\displaystyle y^{2}=x^{3} ax b}$ (cas supersingulier)

où a, b sont des éléments de K.

• Si la caractéristique de K est 2 (par exemple si K est le corps fini à 2^r éléments) alors l'une des deux simplifications suivantes est applicable :

${\displaystyle y^{2} xy=x^{3} ax^{2} b}$ (cas ordinaire)

${\displaystyle y^{2} cy=x^{3} ax b}$ (cas supersingulier)

où a, b (respectivement, a, b, c) sont des éléments de K.

Notes et références

• Portail de l’algèbre